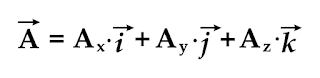Vectores unitarios
Los vectores unitarios, vector normalizado o simplemente versor se pueden expresar en cada una de las dimensiones (1D, 2D y/o 3D) y comúnmente se identifican por las letras "i", "j" y "k" respectivamente para cada eje cartesiano "x", "y" y "z".
En el espacio tridimensional, se utilizan tres vectores unitarios principales para describir la dirección de un vector. Estos vectores se conocen como i, j y k, y representan las direcciones positivas de los ejes x, y y z, respectivamente.
Al combinar diferentes cantidades de estos vectores unitarios, se puede representar cualquier vector en el espacio tridimensional. Entonces un vector unitario tiene una longitud o magnitud igual a 1 y se utiliza para indicar la dirección de un vector sin cambiar su longitud.
Los vectores unitarios sirven para representar la dirección y sentido de cualquier vector, siempre van a tener una magnitud o módulo de uno (1), de ahí su nombre unitario. (También representan el sentido en caso de que se tenga en cuenta el signo, positivo hacia un lado y negativo hacia el otro)
Los vectores unitarios no tienen una dirección específica en sí mismos, sino que su dirección está determinada por la dirección de los ejes cartesianos que representan. Por lo tanto, i, j y k no apuntan en ninguna dirección particular en el espacio, sino que simplemente indican las direcciones positivas de los ejes cartesianos correspondientes. Además son perpendiculares entre sí, en otras palabras significa que i, j y k son ortogonales.
Cuando el vector unitario se encuentra sobre un eje coordenado directamente su magnitud es uno, y en los otros ejes coordenados será cero.
De este modo existen casos donde el vector se encuentra sobre un eje, como a continuación:
En el eje X: i (1); j (0); k (0)
En el eje Y: i (0); j (1); k (0)
En el eje Z: i (0); j (0); k (1)
Cuando el vector unitario se encuentra en una dirección diferente a los ejes coordenados, se deben calcular sus componentes (sus respectivos valores en i, j y k) y la suma de estos tres valores por cálculo de magnitud debe ser uno (1).
Generalmente los vectores unitarios se representan con una u.
La fórmula para calcular el vector unitario es una consecuencia directa de la definición de un vector unitario como un vector de magnitud 1 que apunta en la misma dirección que un vector dado.
Si tenemos un vector cualquiera, podemos obtener su dirección dividiéndolo por su magnitud, ya que el resultado de esta división será un vector que tiene la misma dirección, pero una magnitud de 1. Es decir, la fórmula para el vector unitario:
Por ejemplo una representación del vector "A" y su magnitud vectorial puede ser la siguiente:
Y teniendo en cuenta que la magnitud del vector o el módulo del vector es la magnitud escalar, podemos asumir que "A", es cualquier número que representa la longitud del vector:
Para comprender mejor, por ejemplo, tenemos un vector de magnitud A en un plano 3D con componentes en sus ejes X, Y y Z, entonces, tanto las componentes de los ejes como el vector de magnitud A van a tener su propio vector unitario.
Se dibujan los vectores unitarios de cada vector, los cuales deben estar en la misma dirección y sentido de cada vector.
Si un vector de magnitud A se encuentra en un plano 3D y tiene componentes en todos los ejes, se utilizan los tres vectores unitarios i, j, k; se calcula la parte vectorial y se calcula la parte escalar de dicho vector.
Con estas partes del vector se calcula el vector unitario.
Se divide la parte vectorial entre la parte escalar, obteniendo así el vector unitario con sus componentes en cada eje (valores de i, j, k).
Se comprueba que son válidos estos valores calculando la magnitud o modulo del vector unitario, que debe dar uno (1).
Para comprender lo anterior suponemos un vector "A" que tiene componentes en los tres ejes cartesianos, siendo el valor de la componente en X de 9, el valor de la componente en Y de 6 y el valor de la componente en Z de 2, la parte vectorial del vector "A" será la suma de dichas componentes en los ejes X, Y y Z.
Luego para calcular la magnitud del vector se utiliza el Teorema de Pitágoras aplicado a un plano 3D, mediante la raíz cuadrada de la suma de los cuadrados de sus componentes, lo que resultara en la magnitud escalar o módulo del vector A.
Para calcular el vector unitario del vector A se utiliza la fórmula en la que se divide el valor del vector A entre su módulo o magnitud escalar, obteniendo así el vector unitario con sus componentes en cada uno de los ejes coordenados.
También se puede comprobar que la magnitud del vector unitario es uno (1), aplicando la raíz cuadrada a la suma de componentes elevadas al cuadrado.