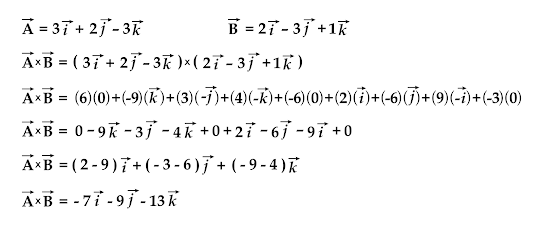Multiplicación de vectores
La operación de multiplicación de vectores puede clasificarse en cuatro tipos: tres de ellos son de tipo vector por vector, mientras que el cuarto tipo es la multiplicación de un vector por un escalar. Estos tipos son los siguientes:
- Producto escalar o producto punto (vector por vector): Es la multiplicación de dos vectores que resulta en un escalar.
- Producto vectorial o producto cruz (vector por vector): Es la multiplicación de dos vectores que resulta en un vector.
- Producto mixto (vector por vector): Es la multiplicación de tres vectores que resulta en un escalar.
- Producto de un vector por un escalar (vector por escalar): Es la multiplicación de un vector por un escalar que resulta en un vector con la misma dirección pero con una magnitud diferente.
Los métodos para solucionar estas operaciones sirven para vectores en cualquiera de las dimensiones, ya sea 1D, 2D o 3D.
Índice
Producto escalar punto (producto punto)
Este es un tipo de multiplicación de un vector por otro vector. Y se representa por un punto entre los vectores a multiplicar, su resultado debe ser de magnitud escalar.
Teóricamente el producto punto de dos vectores es igual a la multiplicación de la magnitud de dichos vectores por el coseno del ángulo entre ellos.
En esta operación es muy importante tener presente el significado de paralelo, el producto punto de dos vectores solo ocurre cuando los vectores a multiplicar son paralelos y se encuentran en un mismo eje o con un mismo vector unitario, es decir el ángulo entre ellos es 0° o 180°.
El producto punto tendrá valor si el ángulo entre los vectores es igual a 0 o 180 grados, dependiendo del ángulo que tengan su resultado cambiará de signo:
- Si el ángulo es 0 grados significa que los vectores van en el mismo sentido, el resultado será positivo.
- Si el ángulo es 180 grados significa que los vectores van en sentido opuesto (el uno con el otro), el resultado será negativo.
Por ejemplo, tenemos dos vectores cada uno sobre los ejes de un plano 2D, si están sobre los ejes no tienen componentes rectangulares.
En el primer caso los vectores son paralelos con un ángulo de 0 grados entre sí, dando como resultado una magnitud escalar positiva.
En el segundo caso los vectores son paralelos con un ángulo de 180 grados entre sí, dando como resultado una magnitud escalar positiva.
También existe el caso en que los vectores son perpendiculares lo que significa que su ángulo es de 90 grados y su producto punto será cero o su valor será nulo.
Si los vectores no se encuentran sobre los ejes, se deben identificar las componentes de cada vector, luego multiplicar dichas componentes entre ellas.
Se debe tener en cuenta los vectores componentes que sean paralelos (con ángulo de 0° o 180°) y los que sean perpendiculares (con ángulo de 90° o 270°).
Un ejemplo de producto escalar punto en dos dimensiones es el siguiente: se tienen dos vectores cada uno con componentes en el eje X y en el eje Y, entonces, serán vectores componentes paralelos los que se encuentren en un mismo eje (con ángulos de 0° o 180°) y perpendiculares en ejes distintos (con ángulos de 90° o 270°).
De lo anterior se puede observar que el resultado de la multiplicación de dos vectores paralelos es un escalar y la multiplicación de dos vectores perpendiculares es cero.
Otra forma de entender esta operación es por medio de vectores unitarios, los vectores que sean iguales tendrán valores de uno (1) o menos uno (-1), mientras que los vectores que sean distintos tendrán un valor igual a cero (0).
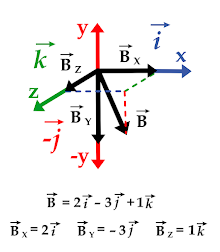
Otro ejemplo de producto escalar punto, pero en tres dimensiones es el siguiente: Se tienen dos vectores cada uno con componentes en el eje X, en el eje Y y en el eje Z, representados con sus respectivos vectores unitarios.
Se multiplican las magnitudes de las componentes que tengan el mismo vector unitario (por ejemplo, i con i).
Recordemos que, si los vectores tienen igual vector unitario el ángulo entre ellos será de 0° (positivo) o de 180° (negativo). El resultado de la multiplicación es una magnitud escalar.
Producto vectorial cruz (producto cruz)
Este es otro tipo de multiplicación de un vector por otro vector. Y se representa por una cruz o equis entre los vectores a multiplicar, su resultado debe ser otro vector.
Teóricamente el producto cruz de dos vectores es igual a la multiplicación de la magnitud de dichos vectores, por el seno del ángulo entre ellos.
En esta operación es muy importante tener presente el significado de perpendicular, el producto cruz de dos vectores solo ocurre cuando los vectores a multiplicar son perpendiculares y se cruzan uno con otro en algún punto formando un ángulo entre ellos de 90° o 270° (ángulo recto); a esto también se le llama vectores ortogonales.
El resultado de esta multiplicación es otro vector que surge perpendicular al plano formado por los vectores anteriores.
Por ejemplo, se tiene un plano X-Y en donde se encuentran los vectores A y B, al multiplicarse resulta la formación de un eje Z sobre el cual se dirige el vector producto de la operación.
Para entender esta operación se identifican las componentes por vectores unitarios, los vectores que sean distintos crean el vector unitario faltante.
Por ejemplo, un vector i multiplicado por uno j tendrá como resultado un vector k.
Mientras que los vectores iguales o paralelos tendrán valores de cero (0).
El siguiente gráfico ayuda a realizar la identificación de la multiplicación a realizar con su respectivo producto.
Cuando se multipliquen dos vectores unitarios se busca el camino más corto sin importar el sentido en el que vaya, ya que según el sentido el producto será positivo o negativo.
Esto quiere decir que también es importante tener en cuenta el orden de los vectores unitarios a multiplicar, es decir, si tenemos un vector 4(i) multiplicado por otro vector 6(k), el orden de los vectores es primero i y luego k.
Supongamos que se necesita multiplicar el vector i con el vector k, el camino más corto será el producto j negativo.
Si se necesitara multiplicar el contrario, es decir, el vector k con el vector i, el camino más corto será el producto j positivo.
Si los vectores no se encuentran sobre los ejes, se deben identificar las componentes de cada vector y multiplicar dichas componentes. Se debe tener en cuenta los vectores componentes que sean paralelos (con ángulo de 0°o 180°) y los que sean perpendiculares (con ángulo de 90° o 270°).
Un ejemplo de producto vectorial cruz es el siguiente: Se tienen dos vectores en el espacio, cada uno con componentes en los tres ejes, serán vectores componentes paralelos los que se encuentren en un mismo eje (con ángulos de 0° o 180°) y perpendiculares en ejes distintos (con ángulos de 90° o 270°).
Los anteriores gráficos no están a escala.
El vector resultante es perpendicular a los vectores A y B.
Otra forma de realizar estas operaciones es por medio de matrices utilizando la función determinante de tercer orden. Se deben conocer los valores de las componentes, en caso de que alguna componente no tenga valor se coloca cero (0).
Tomando como ejemplo los vectores anteriores y resolviendo por matrices, se obtiene que:
El resultado es el mismo que en el ejemplo anterior, el vector resultante es perpendicular a los vectores A y B.
Producto mixto
El producto mixto es una forma de multiplicar tres vectores y básicamente utiliza los dos métodos anteriores, el producto escalar punto y el producto vectorial cruz.
Se utiliza primero el producto vectorial y luego se hace el producto escalar.
Primero se deben multiplicar los dos primeros vectores por medio del producto vectorial cruz, aplicando determinantes a los vectores se halla el valor del vector resultante de sus respectivos componentes.
Luego el vector resultante de dicha operación multiplica al último vector por medio de producto escalar punto.
El resultado de dicha operación es una magnitud escalar.
Producto de un vector por un escalar
Esta es una operación de un vector por un escalar, básicamente se multiplica una magnitud escalar con una magnitud vectorial (un vector), obtenido de resultado otra magnitud vectorial (otro vector).
El vector resultante de esta operación tendrá una magnitud igual a la multiplicación de magnitudes escalares y la dirección del vector multiplicado, el sentido lo definirá el signo.
Se multiplica la parte escalar del vector por el escalar dando como resultado la parte escalar del vector resultante.
La dirección es la misma que la dirección del vector multiplicado.
Si el escalar lleva signo positivo el vector resultante tendrá el mismo sentido del vector multiplicado, pero si el escalar lleva signo negativo el vector resultante tendrá el sentido opuesto del vector multiplicado.
Cuando el vector a multiplicar tiene componentes, el escalar se debe multiplicar por cada una de las componentes.