Vectores en tres dimensiones
Los vectores en tres dimensiones son una herramienta matemática útil para
describir magnitudes físicas que tienen una dirección y sentido específico en un espacio tridimensional. Estos vectores pueden ser representados en tres planos diferentes, cada
uno de ellos con dos ejes cartesianos que permiten definir las componentes
del vector (plano X-Y, plano X-Z y plano Y-Z).
Al graficar un vector en tres dimensiones se presentarán unas componentes rectangulares a los ejes del plano, una magnitud, una dirección y un sentido.
Índice
Componentes de un vector en tres dimensiones
Un vector en tres dimensiones se puede descomponer en tres componentes: la componente en X, la componente en Y y la componente en Z. Estas componentes representan la proyección del vector en cada uno de los tres ejes cartesianos, que son los ejes X, Y y Z.
Las componentes de un vector en 3D se pueden expresar utilizando coordenadas o utilizando vectores unitarios:
- Las coordenadas son los puntos que se dan para ubicar al vector. A partir de las coordenadas de un vector en los tres ejes se podrá calcular la magnitud de dicho vector. La representación de las componentes se expresa de la siguiente manera:
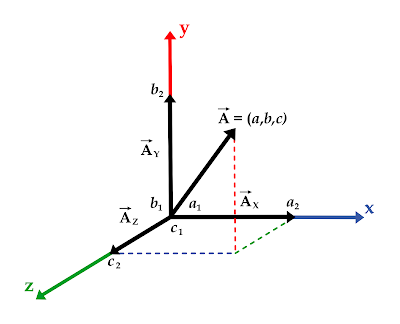
En este caso se asume un orden de X,Y, Z, donde a, b, y c son los puntos de cada uno de los ejes respectivamente y con estos se calcula la longitud (magnitud escalar) del vector sobre dicho eje.
Es decir, los puntos a1 y a2 representan la longitud del vector "A" en el eje X, mientras que b1 y b2 representan la longitud del vector "A" en el eje Y, y los puntos c1 y c2 representan la longitud del vector "A" en el eje Z.
El vector A también lo podemos representar en cada uno de los planos que componen un espacio tridimensional.
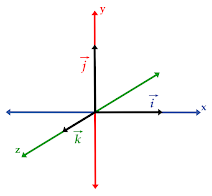
- Los vectores unitarios van a indicar el eje hacia el que va dirigido la componente, entonces, la magnitud o módulo de un vector unitario sobre los ejes es de uno (1). La representación de las componentes por vectores unitarios se expresa así:
En este caso los términos a, b y c representan la magnitud escalar que tiene el vector en cada eje, y los términos i, j y k representan la parte vectorial y dirección.
Magnitud o módulo en tres dimensiones
La magnitud o módulo de un vector en 3D se calcula del mismo modo que se realiza con los vectores en 2D: utilizando los valores de las componentes, en este caso de los tres ejes X, Y y Z.
En caso de que los valores de las componentes del vector se expresen en coordenadas se hace del siguiente modo:
En caso de que los valores se expresen por medio de los vectores unitarios o por valores directos de las componentes, se realiza del siguiente modo:
Dirección y sentido de un vector en tres dimensiones
Determinar la dirección y sentido de un vector es importante para entender y describir el movimiento y la fuerza de los objetos en el espacio tridimensional. La dirección nos indica la inclinación (o ángulo) de la línea de aplicación del vector en el espacio, mientras que el sentido nos indica la orientación en la que se desplaza el vector.
Existen algunas maneras para determinar la dirección y sentido de un vector en tres dimensiones:
- Mediante la utilización de vectores unitarios
- Mediante cosenos directores
Vectores unitarios en tres dimensiones
Un vector unitario es aquel que posee una longitud igual a 1 y está orientado en una dirección particular dentro del espacio tridimensional. Por tanto, se trata de un vector que no presenta una magnitud específica, sino que solo indica la dirección en la que se extiende.
Para obtener un vector unitario que apunte en la dirección de cualquier vector dado, se divide ese vector entre su magnitud. De esta forma, se obtiene un vector con la misma dirección que el vector original, pero con una longitud de 1. Es decir, se normaliza el vector dividiéndolo por su magnitud para obtener un vector unitario.
Para conocer más acerca de vectores unitarios, haz clic en el siguiente enlace:
Cosenos directores
Los cosenos directores expresan la dirección de los vectores sobre cada eje de algún plano (un sistema de coordenadas cartesianas). De esta forma los cosenos relacionan los ángulos que el vector tiene respecto a los ejes en el sentido positivo de cada eje coordenado.
En un sistema de coordenadas cartesianas tridimensional, la suma de los cuadrados de los cosenos directores de un vector siempre es igual a uno (1). A esta propiedad se le conoce como la identidad de Pitágoras en tres dimensiones.
A partir de razones trigonométricas se puede establecer la relación entre el vector, sus componentes y el coseno del ángulo respecto a cada uno de los ejes del plano tridimensional.
Para conocer más acerca de cosenos directores, haz clic en el siguiente enlace:
Suma o resta de vectores en 3 dimensiones
La suma o resta de vectores en 3D puede ser un proceso sencillo si se identifican correctamente las coordenadas o componentes de los vectores y se entiende su orientación en el espacio tridimensional. Para realizar estas operaciones, es esencial conocer el sentido de los vectores y cómo afectará a la operación.
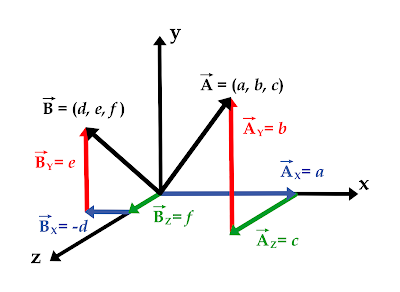
Una forma eficiente de sumar o restar vectores en 3D es descomponer los vectores en sus componentes a lo largo de cada eje (x, y, z) utilizando los correspondientes vectores unitarios (i, j, k). Luego, se agrupan las componentes por eje y se suman o restan entre sí para obtener las componentes del vector resultante.
Es importante recordar que la dirección y sentido del vector resultante dependerá del valor y signo de cada componente. Si se quiere determinar la magnitud y dirección del vector resultante, se puede utilizar la fórmula de la magnitud del vector y la fórmula de los cosenos directores.
En la suma o resta de vectores lo principal es saber identificar las coordenadas o componentes de los vectores, también es importante conocer el sentido que tienen en el plano con el fin de determinar el signo que tendrá en las operaciones. Lo mejor para sumar o restar vectores en tres dimensiones es realizar estas operaciones por medio de sus componentes.
Otra forma en que se den los vectores al momento de sumar o restar es por su magnitud y ángulos, teniendo que calcular la componente en cada eje.
Para calcular las componentes es necesario tener en cuenta los ángulos que se forman en cada plano (X-Y, X-Z, Y-Z) y saber con respecto a que eje se encuentran definidos.
Se utilizan las identidades trigonométricas como cosenos, senos, tangente y otros métodos de trigonometría para calcularlos.
Luego de calcular cada componente de cada vector, se realiza la suma o resta de los vectores por componentes agrupándolos según su vector unitario.
Ejercicios resueltos de vectores en tres dimensiones
¡Felicitaciones por haber llegado hasta aquí! Esto significa que has leído la teoría anterior y tienes las bases completas para comprender mejor el tema de vectores. Espero que hayas anotado un listado con las fórmulas que se utilizan para los vectores en dos y tres dimensiones porque a continuación, podrás practicar este tema con una lista de ejercicios resueltos sobre vectores.
Espero te sirvan de ayuda <3