Suma o resta de vectores en dos dimensiones
Las operaciones de suma y resta de vectores en un plano de dos dimensiones se dividen en: operaciones con dos vectores y operaciones con más de dos vectores; para cada caso existen diferentes maneras de solucionarlas.
Índice
Suma o resta de dos (2) vectores
La suma o resta de dos vectores va estar determinado por el signo que lleven los vectores, o por los signos del enunciado de la operación, por ende, en algunos casos la operación podría verse como una resta, pero volverse una suma y viceversa.
Los métodos para solucionar dichas operaciones se clasifican en métodos gráficos y métodos analíticos.
1. Métodos gráficos
Sirven para resolver las operaciones de suma o resta, utilizando la capacidad de medir por medio de reglas o algún otro instrumento de medición y de toma de datos.
Método del triángulo (método gráfico)
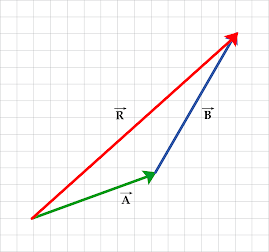
El método del triángulo o método de cabeza – cola, es utilizado para calcular la suma o resta de dos vectores mediante la representación gráfica, permitiendo calcular la resultante de esta operación.
Consiste en formar un triángulo por medio de dos vectores los cuales van a estar unidos cabeza con cola, dando como resultado el vector resultante “R” que unirá la cola del primero con la cabeza del segundo.
Procedimiento
Primero se debe identificar que magnitud, sentido y dirección tienen los vectores, también se debe tomar un sistema medible y una escala (mm, cm, m, etc.) que va estar aplicado a las gráficas.
Luego se coloca el primer vector sobre algún punto de referencia con las medidas y la dirección o ángulo correctos.
Seguidamente se coloca el segundo vector sobre la punta o cabeza del primer vector como si fuera su punto de referencia, de igual forma con las medidas y la dirección o ángulo correctos.
Por último, se grafica el vector resultante partiendo desde el punto de referencia (o cola) del primer vector y terminando en la cabeza del segundo vector.
Luego se mide la magnitud y dirección (ángulo) de la resultante y ese va ser el resultado de la operación suma de dos vectores por medio del método del triángulo.
En cuanto al orden de los vectores no importa (se aplica la propiedad conmutativa), se puede graficar cualquiera de los dos vectores primero. Es decir, en el ejemplo anterior se puede colocar inicialmente el vector B y luego el vector A y el resultado debe dar el igual.
Se debe tomar en cuenta que el ángulo se toma desde el eje x para mejor realización.
Método del paralelogramo (método gráfico)
El método del paralelogramo también es utilizado para calcular la suma o resta de dos vectores, utilizando la representación gráfica para calcular la resultante.
Consiste en formar una figura geométrica de cuatro lados uniendo dos vectores desde sus colas y luego colocando los mismos vectores en paralelo, el vector resultante será el que una las colas con las cabezas de los vectores.
Procedimiento
Primero se debe identificar que magnitud, sentido y dirección tienen los vectores, también se debe tomar un sistema medible y una escala (mm, cm, m, etc.) que va estar aplicado a las gráficas.
Luego se coloca el primer vector sobre algún punto de referencia con las medidas y la dirección o ángulo correctos.
Se coloca el segundo vector sobre el mismo punto de referencia que el primero (con las medidas y la dirección o ángulo correctos) de modo que queden unidos por sus colas.
Se debe graficar los mismos dos vectores sobre las cabezas de los primeros y en paralelo a ellos, quedando una figura totalmente cerrada.
Por último, se grafica el vector resultante uniendo las colas de los primeros vectores con las cabezas de los segundos vectores.
Luego se mide la magnitud y dirección (ángulo) y ese va ser el resultado de la operación de dos vectores por medio del método del paralelogramo.
También es posible utilizar este método para realizar operaciones de suma o resta con más de dos vectores, siguiendo el procedimiento de a dos vectores y no todos al tiempo.
Es decir, si se quisieran sumar cuatro (4) vectores con este método primero se deben suman dos, luego la resultante de esos dos se suma con el tercero, la resultante de la operación anterior se suma con el cuarto vector y la resultante de esa última suma será el resultado final de toda la operación.
|
|
Ejemplo de suma de cuatro vectores por el método del paralelogramo: |
Nótese que no importa el orden para sumar o restar los vectores (se aplica la propiedad conmutativa), se puede graficar primero cualquiera y obtener el mismo resultado.
Además siempre los vectores dibujados en paralelo tienen que corresponder y ser iguales a los primeros vectores.
Se debe tomar en cuenta que el ángulo se toma desde el eje x para mejor realización.
2. Métodos analíticos
Son métodos en los que se realizan operaciones matemáticas y muchas veces van acompañados de gráficos para un mejor entendimiento y análisis.
Ley o teorema de senos (método analítico)
La ley o teorema de senos se aplica para cualquier triángulo mediante una relación de ángulos y lados (se utiliza principalmente para triángulos no rectángulos u oblicuos).
Este método relaciona la longitud de un lado del triángulo al seno del ángulo opuesto a ese lado, del mismo modo se hace para todos los lados y ángulos en el triángulo dado.
Para poder utilizar este método es necesario que se tengan al menos tres datos del triángulo, es decir, saber el valor de dos ángulos y un lado o el valor de dos lados y un ángulo.
Para conocer más acerca de la Ley de Senos o Teorema de Senos, haz clic en el siguiente enlace:
Ley o teorema de cosenos (método analítico)
La ley o teorema de cosenos es utilizada para cualquier triángulo mediante una relación de ángulos y lados (se utiliza principalmente para triángulos no rectángulos u oblicuos).
Contrario a la ley de senos este método utiliza las longitudes de los lados y ángulos en combinación.
|
|
- Fórmula relacionando los tres lados A, B y R, además del ángulo entre
A y B (Theta). - Fórmula relacionando los tres lados A, B y R, además del ángulo entre B y R (Alfa). - Fórmula relacionando los tres lados A, B y R, además del ángulo entre A y R (fi). |
Este método se puede utilizar en los casos donde las medidas de dos lados y el ángulo entre ellos son conocidas o en el caso donde se conozcan los tres lados del triángulo.
Para conocer más acerca de la Ley de Cosenos o Teorema de Cosenos, haz clic en el siguiente enlace:
Suma o resta de más de dos (+2) vectores
Existen los casos en que las operaciones involucran a más de dos vectores y que no se les puede aplicar métodos como el del triángulo o paralelogramo, ni la ley de senos o cosenos directamente, sin embargo, existen otros métodos parecidos a los anteriores utilizados para la solución de estas operaciones.
Método del polígono (método gráfico)
Este método se realiza por medio de la representación gráfica, donde es muy importante la exactitud con la que se dibujen los vectores y se grafiquen los valores, todo esto a mano alzada, al igual que todos los métodos gráficos.
Básicamente se grafican los vectores a una escala medible, uno después del otro y al final se traza un vector resultante uniendo la cola del primer vector con la cabeza del último vector.
Procedimiento
Primero se debe identificar que magnitud, sentido y dirección tienen los vectores, también se debe tomar un sistema medible y una escala (mm, cm, m, etc.) que va estar aplicado a las gráficas.
Luego se coloca el primer vector sobre algún punto de referencia con las medidas y la dirección o ángulo correctos, sucesivamente se van colocando todos los demás vectores uno por uno comenzando en la cabeza del anterior (con las medidas y la dirección o ángulo correctos) de modo que queden unidos por su cola-cabeza.
Por último, se grafica el vector resultante partiendo desde el punto de referencia del primer vector o la cola y termina en la cabeza del último vector.
Luego se mide la magnitud y dirección (ángulo) y ese va ser el resultado de la operación de dos vectores con el método del polígono.
En cuanto al orden de los vectores no importa (se aplica la propiedad conmutativa), se puede graficar cualquiera de los vectores primero.
Se debe tomar en cuenta que el ángulo se toma desde el eje x para mejor realización.
Descomposición vectorial (método analítico)
La descomposición vectorial básicamente consta en separar y sumar las componentes de cada vector según los ejes X o Y, obteniendo así las componentes de la resultante.
Luego por medio de Pitágoras u otros conceptos de trigonometría se halla el valor de la resultante (la magnitud), con su respectiva dirección y sentido.
Este método se puede utilizar para sumar dos o más vectores.
Supongamos una suma de 5 vectores representados en un plano X-Y ubicados del siguiente modo:
Se identifican los vectores con componentes en X y en Y, también los vectores que se encuentran sobre los ejes X y Y; se debe tener claro los signos que llevan según la ubicación, dirección y sentido en el plano.
Se hace una sumatoria de vectores por componentes en X y otra a parte en Y, dando como resultado las componentes del vector resultante en cada eje.
Por último, por medio del teorema de Pitágoras se calcula el valor de la resultante y su respectivo ángulo.
