Ejercicios presión y manómetros

Más ejercicios: I 1 I 2 I 3 I 4 I

Examine el sistema de la figura P1-86. Si un cambio de 0.7 kPa en la presión del aire causa que baje 5 mm la interfase entre salmuera y mercurio, en la columna derecha, mientras que la presión en el tubo de salmuera permanece constante, determine la relación A2/A1.

La parte superior de un recipiente de agua está dividida en dos compartimientos, como muestra la figura P1-85. En un compartimiento se vierte líquido de densidad desconocida, y el nivel del agua sube cierta cantidad en el otro compartimiento, para compensar este efecto. De acuerdo con las alturas finales de líquido que muestra la figura, calcule la densidad del líquido agregado. Suponga que el líquido no se mezcla con agua.

La presión manométrica en el recipiente de aire de la figura P1-83 es 80 kPa. Calcule la altura diferencial h de la columna de mercurio.

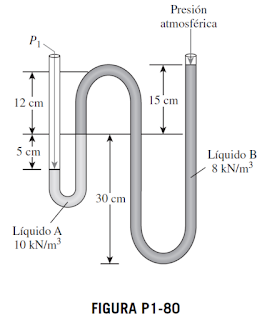
Calcule la presión absoluta P1, del manómetro de la figura P1-80, en kPa. La presión atmosférica local es 758 mm Hg.

Agua dulce y de mar fluyen en tuberías horizontales paralelas conectadas entre sí mediante un manómetro de tubo en doble U, como se muestra en la figura P1-78. Determine la diferencia de presión entre las dos tuberías, considerando la densidad del agua de mar a ese punto de ρ = 1 035 kg/m3. ¿Se puede ignorar la columna de aire en el análisis?

Considere un tubo en U cuyas ramas están abiertas a la atmósfera. Ahora se agrega agua dentro del tubo desde un extremo y aceite ligero (ρ = 790 kg/m3) desde el otro. Una de estas ramas contiene 70 cm de agua, mientras que la otra contiene ambos fluidos con una relación de altura aceite-agua de 4. Determine la altura de cada fluido en esta rama.

Determine la presión que se ejerce sobre un buzo a 30 m debajo de la superficie libre del mar. Suponga una presión barométrica de 101 kPa, y una gravedad específica de 1.03 para el agua de mar.

La presión arterial máxima en la parte superior del brazo de una persona saludable es de alrededor de 120 mm Hg. Si un tubo vertical abierto a la atmósfera se conecta a la vena del brazo, determine cuánto ascenderá la sangre en el tubo. Considere la densidad de la sangre como 1 050 kg/m3.

El piloto de un avión lee una altitud de 9 000 m y una presión absoluta de 25 kPa cuando vuela sobre una ciudad. Calcule en kPa y en mm Hg la presión atmosférica local en esa ciudad. Tome las densidades del aire y el mercurio como 1.15 kg/m3 y 13 600 kg/m3, respectivamente.

La fuerza generada por un resorte está dada por F =  kx donde k es la constante del resorte y x su deformación. El resorte de la figura P1-95 tiene una constante de 8 kN/cm. Las presiones son P1 = 5.000 kPa, P2 = 10.000 kPa y P3 1 000 kPa. Si los diámetros del émbolo son D1 8 cm y D2 3 cm, ¿cuál será la deformación del resorte?

Un recipiente con varios líquidos se conecta con un tubo en U, como se ve en la figura P1-87. Para las gravedades específicas y alturas de columna indicadas, calcule la presión manométrica en A. También determine la altura de una columna de mercurio que causara la misma presión en A.

Más ejercicios: I 1 I 2 I 3 I 4 I