Ley de senos o teorema de senos
La ley o teorema de senos se aplica para cualquier triángulo mediante una relación de proporcionalidad de sus lados y de los senos de los ángulos que existen entre ellos (se utiliza principalmente para triángulos no rectángulos u oblicuos).
Este método relaciona la longitud de un lado del triángulo al seno del ángulo interior opuesto a este lado, del mismo modo se hace para todos los lados y ángulos en el triángulo dado.
Para poder utilizar este método es necesario que se tengan al menos tres datos del triángulo, es decir, saber el valor de dos ángulos y un lado opuesto a estos o el valor de dos lados y un ángulo opuesto a estos.
Por ejemplo, los valores de dos lados (A y R) y el valor del ángulo opuesto al lado R (theta) para poder hallar el ángulo de la fracción de A (alfa).
De este modo luego de identificar qué relaciones se deben utilizar, se reemplazan los valores y se despeja en función de la incógnita para encontrar su valor.
De igual manera se puede utilizar cualquiera de las tres fracciones, solo se requiere que cumplan la condición del número de valores e incógnitas (saber el valor de dos ángulos y un lado opuesto a ellos o el valor de dos lados y un ángulo opuesto a ellos ).
En caso de conocer el valor de dos ángulos, se puede hallar el valor del tercero estableciendo que la suma de sus tres ángulos debe ser igual a 180 grados. Por lo tanto se puede restar a 180 grados la suma de los dos ángulos conocidos y el resultado será el tercer ángulo.
Demostración Ley o Teorema de Senos
Para demostrar la fórmula general del teorema de senos es necesario colocar un triángulo en una circunferencia (a esto se le llama triángulo inscrito en una circunferencia), lo cual consiste en dibujar la circunferencia pasando por todos los vértices del triángulo a estudiar.
Se supone un triángulo cualquiera en el que se identifican sus lados "a", "b" y "c" y sus respectivos ángulos internos opuestos Alfa, Fi y Theta. Luego se dibuja la circunferencia sobre los vértices de dicho triángulo del siguiente modo.
Se debe tener en cuenta que para la circunferencia de radio "R" se establece que su diámetro es igual a dos veces "R".
Ahora se modifica el triángulo inscrito dejando un lado en la misma posición y tamaño (en este caso será el lado "a"), pero haciendo que un lado pase por el centro de la circunferencia causando que su ángulo opuesto se vuelva un ángulo recto (de 90 grados), de este modo surgen dos nuevos lados llamados "x" y "z".
El ángulo Alfa no cambia debido a que para el triángulo inscrito en la circunferencia el lado "a" va contar con un "ángulo de visión" o "amplitud de ángulo" de igual magnitud en todos puntos de dicha circunferencia, a esto se le conoce como Arco Capaz.
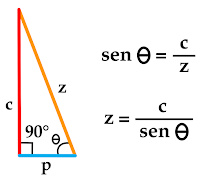
De este modo para el triángulo rectángulo se puede definir la función trigonométrica de seno del ángulo Alfa igual al cateto opuesto (lado "a") entre la hipotenusa (lado "z"). Si se despeja "z" de la función se puede observar la primera fracción de la fórmula general.
Se repite el proceso con el triángulo inscrito dejando el lado "b" en la misma posición y tamaño, haciendo que un lado pase por el centro de la circunferencia, obteniendo dos nuevos lados llamados "y" y el mismo lado del triángulo anterior, lado "z". En este caso el ángulo opuesto al lado "b" no cambia.
Para este triángulo rectángulo se define la función trigonométrica de seno del ángulo Fi igual al cateto opuesto (lado "b") entre la hipotenusa (lado "z"). Si se despeja "z" de la función se observa la segunda fracción de la fórmula general.
Se repite el proceso para el lado sobrante "c" dejándolo en la misma posición y tamaño, haciendo que un lado pase por el centro de la circunferencia, obteniendo dos nuevos lados llamados "p" y el mismo lado del triángulo anterior, lado "z". El ángulo opuesto al lado "c" no cambia.
Para este triángulo rectángulo se define la función trigonométrica de seno del ángulo Theta igual al cateto opuesto (lado "c") entre la hipotenusa (lado "z"). Despejando "z" de la función se observa la tercera fracción de la fórmula general.
Ahora se sabe que el lado "z" es la hipotenusa de los triángulos rectángulos y que a su vez coincide con el diámetro de la circunferencia mostrados anteriormente, por lo que se establece que la hipotenusa es igual al diámetro o a dos multiplicado por el radio de la circunferencia.
Entonces las tres fracciones se igualan al diámetro de la circunferencia que es igual a "2R".
De este modo se demuestra la fórmula general de la ley o teorema de senos.
Relación del Teorema de Senos con Área de un Triángulo Inscrito en una Circunferencia
También es posible demostrar la relación que existe entre el teorema de senos y la fórmula del área de un triángulo.
El área de cualquier triángulo se puede calcular mediante la multiplicación de la base por la altura divididos en 2.
Si se relaciona el área con el teorema, la fórmula se convierte en la multiplicación de los tres lados del triángulo divididos en 4 que multiplica el radio de la circunferencia en que se encuentra inscrito el triángulo.
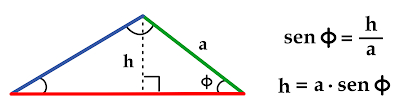
Se toma el triángulo rectángulo formado con la línea de la altura (h) y se aplica la razón trigonométrica de seno del ángulo (Fi), siendo este igual al lado opuesto (h) dividido en la hipotenusa (a).
Se despeja el lado opuesto (h) de la ecuación, observando la multiplicación entre la hipotenusa (a) y el seno del ángulo (Fi).
Tomando la fórmula del área del triángulo se reemplaza la base por el lado que le corresponde (en este caso el lado "c") y se reemplaza la altura (h) por la multiplicación entre la hipotenusa (a) y el seno del ángulo (Fi). La ecuación queda así:
Del teorema de senos se toma la fracción que incluya el seno del ángulo "Fi" y para que se reemplace en la ecuación del área se despeja el seno observando la división entre el lado "b" y 2 por el radio "R".
Se reemplaza el seno del ángulo en la ecuación del área, se realizan las operaciones y se ordenan las variables, obteniendo la demostración de la fórmula del área.
La fórmula del área de un triángulo inscrito en una circunferencia queda así: